Flip-Pin Laser Lattices
A project from Haystack Labs 2024.
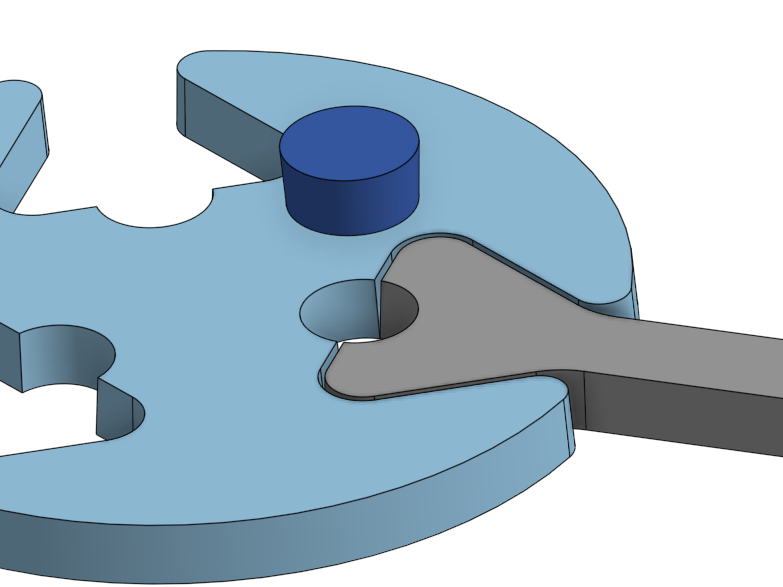
Flip-pin laser lattices are structures press-fit together from laser-cut plywood. No glue is used during assembly, so they can be taken apart with some care. The first (and only) one I’ve made is quite spindly, but one could imagine modifying various dimensions to sturdy up the structure. The lattices are constructed from long strut pieces and round node pieces, which interlock with a dovetail and get secured with an orthogonal pin:
I decided to make a soccer ball shape, a truncated icosahedron. One can imagine this shape as a spherical arrangement of twelve regular pentagons, each surrounded by connected rings of regular hexagons. I made it about half way through before running out of time, as this was a last-day-at-Haystack project, so the project became a dome on the Gateway pin-up wall, as seen in the first image.
Ainsley got a few shots of the assembly process, two of which I will share here (thank you for taking pictures!):
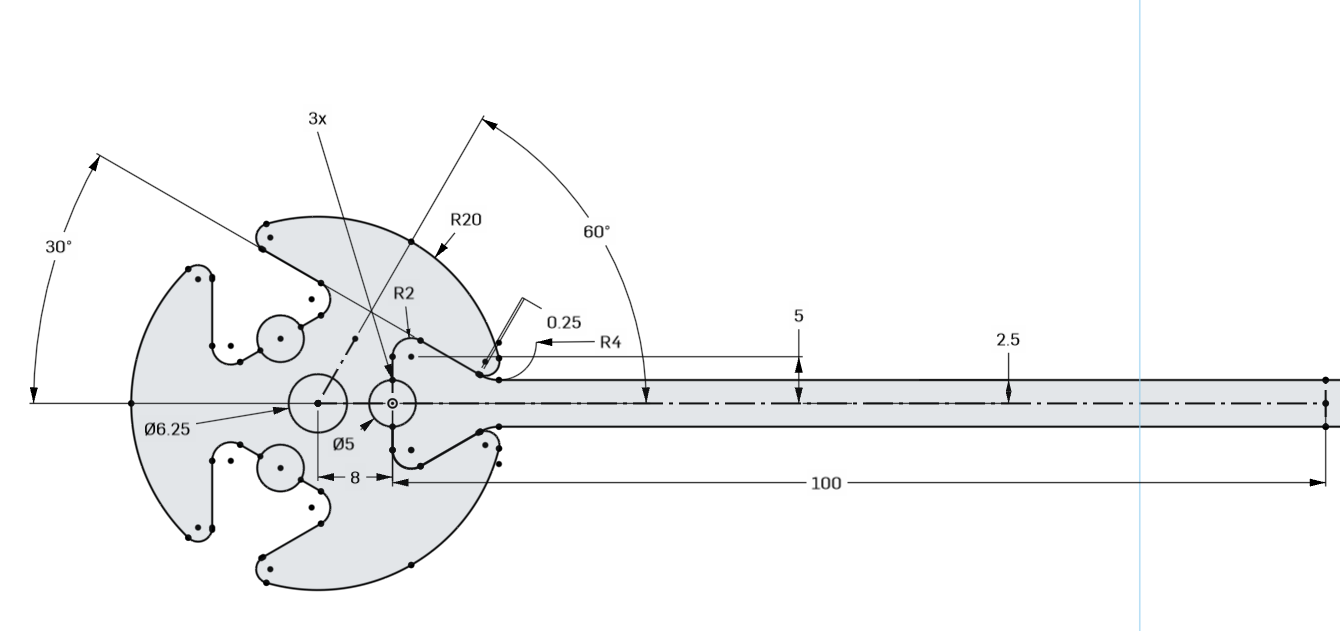
These lattices use joints like the larger caning peg lattices I've worked on since last summer (2023), or the metal version I made a few years ago and brought to the first Labs. The parts are held together using dovetail joints secured by tapered pins inserted during assembly. The joint is then tensioned using a pair of parallel-jaw pliers borrowed from (and returned to) the metals studio. Here is the Onshape sketch I used to define the geometry, noting that the strut is mirrored to the right off-screen and all dimensions are in millimeters:
The hole in the middle is fabricated as a separate part, and becomes the orthogonal pin which secures the lattice together. Aha! And here is where the interesting part is! Laser cutters produce a slight bit of taper in their parts, so with our particular laser settings the inverted pin just barely fits in the joint:
Well, that is the idea, at least. I did a bunch of tests with the 3.15 mm plywood on hand, using the larger laser cutter at 100% power, 6.5% speed, and 300 PPI, and what I believe is a 2” focal length lens. I was able to make a good joint by cutting the pin 1.25 mm oversize, so 6.25 mm OD for a nominal 5 mm ID strut/node hole. In retrospect, going a tiny bit smaller would probably make assembly easier and not have a huge effect on strength. But it did work!
I eventually made and assembled 53 struts, 36 nodes, and 106 pins. Notably, this represents substantially faster fabrication and assembly (at least in terms of time per unit of structural complexity) as compared to the caning peg lattice project, where I spent more time fabricating fewer parts by a factor of ~5. During the assembly process perhaps 20 pins broke, usually because they went in crooked and lost a bit of material upon squishing with parallel-jaw pliers. My cut files filled empty space with extra pins, so this didn’t become a huge delay beyond re-doing a joint. In one case, mis-inserting the pin caused enough damage to a node that I scrapped that part too. And the most interesting failure occurred near the end of the assembly process, when a strut snapped! Soccer balls are pretty distorted and the pins are quite spindly (only 5 mm wide!), but this was still exciting with not much time before displaying the thing; I was briefly worried that the whole thing would fall apart, but I replaced the strut and it was all good. Maybe a spindly-er aspect ratio would be okay.
I never weighed the ball, but assuming birch, Onshape tells me the struts, nodes, and pins weigh 2.24, 1.72 g, and 0.06 g, respectively. So the partial ball should weigh around 187 g. I also calculated the diameter by plugging the node-center-to-node-center distance of 216 mm into a truncated icosahedron calculator I found online, which told me that the diameter of the ball is roughly 1.06 m, or ~42 inches. A full truncated icosahedron has 90 struts, 60 nodes, and 180 pins, so such a ball would weigh around 316 g. The volume of the ball is around 0.624 m^3; an equivalent volume of air would weigh about (1.204 kg / m^3) * (0.624 m^3) = 751 g. So lighter than air! But not as light as helium, which would weigh about (0.179 kg / m^3) * (0.624 m^3) = 112 g.
Could this serve as the frame for a helium balloon, where the panels are glued-on tissue paper or some other suitable lightweight material? Wikipedia tells me that the surface area of a truncated icosahedron is roughly 72.6a^2, where a is the edge length. As each strut is 0.216 m, that means the surface area is roughly 3.39 m^2 (!!). Maybe I can't find nice tissue paper and I use old newspaper, this website suggests the material may weigh 40-50 g/m^2. In the worst case, that means the paper adds 170 g to the total weight. A helium balloon would weigh roughly 316 + 112 + 170 = 598 g. So it should float, with ~150 g of payload room to spare, some of which will get taken up by glue and poor calculations. It would have to be quite well sealed, helium is tiny! Maybe aluminized mylar is a better call. But then it's just a silver balloon.
What about hot air? How hot would we need to make the air inside the envelope to make it float? Probably pretty hot. The air could only take up 751 - (316 + 112) = 323 g in the balloon, meaning it would need to have a density of 323 g / 0.624 m^2 = 0.518 kg / m^3. We could calculate the exact value with the ideal gas law, or just look at a chart we found online and see it's around 400 C. I think that is too close to the ignition temperature of the wood, and would probably mess up the glue and paper too.
But this is a square-cube problem, right? How big would the balloon need to be to be liftable by reasonably friendly hot air? Some rando articles that didn't include units said most hot air balloons run at 250-300 degrees; assuming that means F, and staying conservative with the paper, maybe we shoot for a 250 F (~120 C) operating temperature. That means an air density of around 0.9 kg / m^3. Onshape's material library estimates birch at 700 kg / m^3, and we're calling paper 50 g / m^2. Paper weight scales with the surface area of the solid, but what about strut, node, and pin weight? Within some range of strut lengths, the nodes and pins stay the same, the material thickness doesn't change, and struts just lengthen, so their weight scales linearly with length. I'm going to come back to this when I am feeling a bit more mathy.
next
Next! What next! Well, a balloon of some kind, probably. I’d like to try making the same lattice out of ¼” plywood, since that would allow me to cut the pins a bit smaller while still having plenty of insertion length to tension the joint. Right now, everything is kind of jammed together, and probably not practically reversible for this reason. I might also try just making the pins out of thicker plywood, which would save on fabrication time and weight but would probably require a custom assembly tool (oh no…). Given the strut failure I saw earlier, I might be near the soccer ball aspect ratio limit for the material thickness; in other words, to allow sufficient lattice distortion for a truncated icosahedron, I might need to make the struts twice as long (~400 mm, which is long). So perhaps trying to stick with ⅛” stock is wise. I do want to try a complex curve! And maybe some weird (and limited) hyperbolic shapes, à la HyperRogue.
Then, lots of parts! Lots lots lots. With enough tools and parts and a few minor design improvements, I bet most folks could assemble a few joints per minute, so a crew could make a really interesting sizable structure in a few hours with enough struts, nodes, and pins. At least a few balls and maybe a capped tube or two. Tubes would be fun: we could do experiments with armchairs and zigzags for teaching people about carbon nanotubes and chirality! “Plywood Mesotubes” or something.
license
I haven't established a repository dedicated to tracking files related to this project; right now there is just the linked CAD file with the dimentioned sketch, and the text and images on this page (which is part of my portfolio website's repo). The Flip Pin Laser Lattice project is very much a work-in-progress, so there will be more to come; for the time being, I am releasing all of the files related to the project (other than pictures attributed to others) under the terms of CC-BY-SA 4.0. So! Go build lattices, and if you do, please tell me your fabrication parameters so I can start keeping track of pin diameter offsets and strut lengths (and link to your project!)!
© copyright zach fredin, 2024